�Љ�S���w����u�`�F�@�u�`����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�Q�O�O�O�N�@�T���P�P���i�ؗj�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���؉p��
2.�Љ�S���w�ɂ�����V�~�����[�V�����̗��p
2.1. �Љ�I�F�m�iillusory correlation�A�O�W�c�̋ώ����F�m�j 5/11
2.2. �Љ�I�e���iSocial Impact ���_�j 5/18, 25
2.3. �W�c�ߒ��i�W�c���c�A�R�~���j�P�[�V�����l�b�g���[�N�j 6/1
2.4. �ΐl�ߒ��i�F�l�E�����W�j 6/8
2.1�@�Љ�I�F�m
���J�j�Y���F�L�����f���@�i�L���ˑ��^�̎Љ�I�F�m�j
���ہF�@�W�c�̔F�m
�@ �Q�D�P�D�P�@���둊��
�Q�D�P�D�Q�@�O�W�c�̋ώ����i�̔F�m�j
�Q�D�P�D�P�@���둊��(Illusory Correlation)
�Q�D�P�D�P�D�P�@���둊�ւ̔���
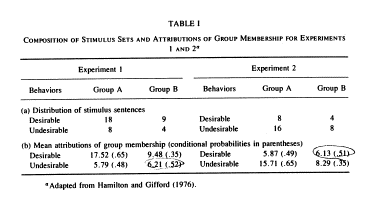
���@Hamilton & Gifford(1976) �̌���
�]���ϐ��@�@ �x������(frequency estimates)
�@�@�@�@�@�@ �肪����Đ�(cued recall)
�@�@�@�@�@�@ ��ە]��(ratings)
�����P�F���W�c�̖]�܂����Ȃ��s���i�����h����j���ߑ�]�������B
�����Q�F���W�c�̖]�܂����s���i�����h����j���ߑ�]�������B

���@���߁F joint distinctiveness
�@�@shared distinctiveness �ijoint distinctiveness�A distinctiveness-based illusory correlation�j
�@�@���W�c�A�����h�@�|�@�Ƃ��� distinctive
�Q�d�� distinctive �Ȃ��̂� differential ��encoding �i����ь����j�������A�L���� availability
�����܂�(Availability heuristics)�B�iChapman, 1967; Tversky, Kahneman ��j
�@�@ �� ���W�c�̏����h�̏o���x���͉ߑ�]�������B
���@����E�L���ˑ��^�̃X�e���I�^�C�v
�@�@�X�e���I�^�C�v�̌`�����iSherman ��j
a. category-level attribute (abstraction-based)
b. instance-based
b-1. on-line processing
b-2. memory-based processing
�@�@Hamilton ��̋c�_�@�|�@instance-based ���� memory-based �ȏꍇ�B
�Q�D�P�D�P�D�Q�@���둊�ւ̈�ʐ�
���@Hamilton ��̌��ʂ͓���ł͂Ȃ�
Hamilton & Gifford(1976) �Ɠ��l�̌��ʂ͑����̌����Ŋm�F����Ă���B
�@�@e.g., Acorn et al.(1988); Feldman et al.(1986); Hamilton, Dugan & Trolier(1985); Pryor(1986);
Sanbonmatsu et al.(1987); Schaller & Maass(1989)
Mullen & Johnson(1990)�F���둊�ւ����肵���������̃��^����
�@�@�肪����Đ����x��p���������|�@�Q�R
�@�@�x�������p���������@ �|�@�Q�W
�@���@���둊�ցi�ӌW���j�͎��ۂɂ���Ɣ��f�ł���B
���@�ȑO����̔ᔻ�@�|�@�r���ł���
��F
�@�P�D�u�����h���]�܂����v�ł� Hamilton �^�̍��둊�ւ͐�����B
�@�Q�D�u��W�c�̑����h�v�̉ߑ�]�������둊�ւ̌����ł͂Ȃ��B
���@�h�������ɂ������ʐ�
�@�����h���́u�]�܂����v�i�m�������{�Љ�����j�̎����ŋL�q����邱�Ƃ������B
�@�������G
�E�Е��̎����i�m�� or �Љ�j�ł����藧�B
�E���̎�����p���Ă� Hamilton �^�̍��둊�ւ͊ώ@���ꂽ�B
�@��F�����^���^���A�y���̃u�����h�̒����E���_�A�������^�W��
���@���둊�ւ͂����ȗv���̉e������B
��F
�P�D���ۂ̑���
�Q�D�h���̋L�q�F�Q�l�I�^�A���I�ibinary/continuous�j�|�Q�l�I�ȏꍇ�ɍ��낪�����B
�R�D���O�̗\���iprior expectation�j�@�`�@encoding �Ȃ����������̕�
�T�D�h�����@�|�@�h�����iN of exemplars�j���傫���قǍ���͋����B
�U�D�W�c���@�|�@��R�̏W�c�����������ƁA�Q�W�c�Ԃ̍��둊�ւ��������Ȃ�
�V�D����̋ɒ[���@�|�@���Ⴊ�ɒ[�ł���قljߑ�]�������B
�W�Dimpression set �i�����j�@�|�@impression set �i����memory set�j�͍����ቺ������B
�X�Dtarget�̑����@�|�@��F�ΏۏW�c�̈���Ɏ�����������ꍇ�A���W�c�т����̘c�݁@
�P�O�Dself-relevance�@�|�@ �����h�ӌ����r�Ɨގ�����iself-relevant�j�ꍇ�A���W�c�ismall town�j�̏����h�ӌ�
���ߑ�]�������X���B
�P�P�D�F�m�ւ̏�Q�@�|�@�F�m�������j�Q������ expectancy-based illusory correlation �������₷���Ȃ�B
�Q�D�P�D�P�D�R�@���둊�ւ̗��_
���@Hamilton ���ishared distinctiveness �ɂ����둊�ցj
���@Fiedler ���F�@information loss + regression
��{�I�A�C�f�B�A�F
�E�m���w�K�ۑ�Ƃ��Ă̍��둊�֎����F�r���͊e�W�c�̓����̔䗦�̊w�K������B
�@��W�c�@�|�@���s���������̂Ŕ䗦�̐���͐��m
�@���W�c�@�|�@�w�K���s�\���B information loss ���傫���B���̌��ʁA�䗦�̐���� regression ��������
�@ �i����䗦�̍����������Ȃ�j�B
�@���@Hamilton �^�̍��둊��
�E���둊�ւ�������ߒ��́A�L���ێ��A�������A�����A�̊e�i�K�Ő�������B
�P�D�L���ێ��i�K�F��W�c����Ə��W�c������e�X�g���ڂƍl����B
�e�X�g���ڐ��������i��W�c�j�̂Ńe�X�g�̐M�����͍����A���肳���ׂ��䗦�̉�A�͏������B
�Q�D�������ؒi�K�FBayesian �� on-line �̉������؉ߒ�
�@�@�@�@�g1�Fpositive �Ȏh���̔䗦�@���@�D�V
�@�@�@�@�g2�Fpositive �Ȏh���̔䗦�@���@�D�R
�@�@�@�@�m �F�V���ȏ��i�V���ɐڐG��������j
�o�i�g1�b�m�j�@�@�@ �@�@�o�i�m�b�g1�j�@�@�@�@�@�o�i�g1�j
�@�@�\�\�\�\�\�\�@���@�\�\�\�\�\�\�@�E�@�\�\�\�\�\�\
�o�i�g2�b�m�j �@�@�o�i�m�b�g2�j �@�@�@ �o�i�g2�j
�@�@�@�@�i����m���̔�j �i�V���ȏ��̉e���j�@�i���O�m���̔�j
�ot�@���@�p�E�ot-1�@�Ƃ����B������
�@�@�@�@�@�@�@�@�@�@�p�@���@ �p�{�@���@0.7/0.3 if �ڐG�������Ⴊ positive
�p�|�@���@0.3/0.7 if �ڐG�������Ⴊ negative
�ڐG��������i���j�̂��� positive �� ��1�Anegative ����2�Ȃ�A �i��1�{��2�����A��1����2�j
�@�@�@�@�@�ot�@���@�p�{t1�E�p�|t2�E�o0�@���@�p+t1-t2�E�o0�D�@�@�@�m��@�p+�E�p�|���P�n
���@negative �Ȏ��ᐔ�ɔ�ׂ� positive �Ȏ��ᐔ�������i��1�|��2����j�قǁA�g1�ւ̊m�M�x�͋����Ȃ�B
�R�D�����i�K�F"central tendency" �� ���W�c�̏����h�̐���l�i�ł��ɒ[�j�ɑ��č�p���₷���B
�x�����錋�ʁFFiedler(1991) �̎����P�`�����S
���@Smith, E.R. �̃V�~�����[�V�������f��
�Q�D�P�D�P�D�S�@Smith, E.R. �̃R���s���[�^�V�~�����[�V����
shared distinctiveness �Ɋ�Â� encoding �����肵�Ȃ��Ă� Hamilton �^�̍��둊�ւ��������邱�Ƃ��A���̃��f���͎����B
���@��{���f��
���@Hintzman(1986)�� Memory Model
�@����h���� traces �� encode ����A�L���ɒ��������B�mstimuli ���@encoding�@���@traces�n
�@�m�o�҂͎h���̑����� features �� sensitive�B
�@features - binary: 1/-1/0(indeterminate)
�o������h���͒����L���i�k�s�l�j�ɋL�^�����B
�@�Y�p�iforgetting�j �|�@�L������ features �������_���Ƀ[���ɂȂ�B
�@�����iretrieval�j�@���@��� probe ���L���ɒ����Ɣ����iecho�j��������B
1. echo intensity = ���� probe �ƋL�����̑S traces �̗ގ����̍��v
2. echo content = ���� probe �̂��Ƃ��ƃ[���������������[������Aa feature vector
���@Hintzmen Memory Model �̕�����
j=1..n: memory trace �� fetures, n=26.
i=1..m: memory �ɒ������ꂽ traces, m=39.
P(j) : probe �� j �Ԗڂ� feature.
T(i,j): i �Ԗڂ� memory trace �� j �Ԗڂ� feature.
�@�ގ����isimilarity�j�F trace i �ɑ��� probe �̗ގ���
�@�@S(i) = 1/NR ��P(j)T(i,j), NR: P(j) �������� T(i,j) �� nonzero �ł��� features ���B
�@�@�@ j
�@�������iactivation�j�Fprobe �ɂ���� trace i ���������������x�B
A(i) = S(i)3.
�L�������iecho intensity�j
I = ��A(i).
i
�L�������iecho content�j�F feature j �ɑ���
�@�@C(j) = ��A(i)T(i,j).
i
����
�@�E�h���̂S�v�f�F�W�c���x���A�l�A�s���^�A����̍s���B
�@�Etrace ���L���ɓ��� �� forgetting�B
�@�E memory will be probed in different ways...
���@���f���̓���
�@�E 26 features�F 6: �W�c���x���i�` or �a�j�A6: ����̏W�c�����A7: �s���^�ipositive or negative�j
7: ����̍s��
�mfeatures �������ɏ��Ȃ��ꍇ�������Afeatures ���͌��ʂɂ����ĉe����^���Ȃ��n
(1) �W�c���x���������_���ɍ��B�efeature�͓����m���� 1 or -1 ���Ƃ�B
�@�@positive �s���^�� feature �l�����l�Ƀ����_���ɍ��Bnegative �s���^�̒l�� positive �̋t�ɂ���B
(2) main simulations: 18A+, 8A-, 9B+, 4B-. -- 39 traces.
Hintzman's full model: �efeature �͊m��L(<=1.0)�ŋL������A�L������Ȃ��ꍇ�̒l�̓[���ɂȂ�B
�@�@�iL = 1.0�Ɖ���j
(3) �Y�p�F�@�m�� 0.3 �ŋL�����ꂽ�e feature ���[���ɂȂ�B
(4) �Q�̏]�����x
1. overall evaluation �i��ۂ��L���ɂ��A�Ɖ���j
�@�@�E �L�����W�c�������� probe ����mprobe �͏W�c���x�� features �����������A���� features �̓[���n�B
�@�@�E�s���^�̋L�������� positive �s���� feature �n��Ƃ̑���(n=7)���Ƃ�B
�@�@�@���@�������ց��W�c�� positive �Ȉ�ہB
2. cued recall
�@�@�E �R�X�̊e�s���� probe �����i�s���^�A����̍s���� features �͊���l�A���̑��̓[���j�B
�@�@�E�e probe �ւ̏W�c���x���̋L�������ƁA�e�W�c�� features �Ƃ̑��ւ��Ƃ�in=6�j�B
�@�@�E ���ւ��������̏W�c�ɂ��̍s�����A������B
�@�@�E�W�c�A���̌��ʂ���ӌW�������߂�B
���@�V�~�����[�V�����̌���
�@�@�ȉ��̌��ʂ��Č������B
�@�@�@1.�ӌW���ƕ]��ɂ����āAHamilton �^�̍��둊�ւ��ώ@���ꂽ�B
�@�@�@2.���둊�ւ̌����͏��W�c�|�����h�̉ߑ�]���ɂ���B
�@�@�@3.�ӌW���͏��W�c�̕]�肾���Ƒ��ւ���B
�@�@�@4.��R�̏W�c������ƍ��둊�ւ͒ቺ����B
�Q�l����
Fiedler, K. 1991, The tricky nature of skewed frequency tables: An information loss account of distinctiveness-based illusory correlations. Journal of Personality and Social Psychology, Vol.60, No.1, 24-36.
Fiedler, K., Hemmeter, U., Hofman, C. 1984, On the origin of illusory correlations. European Journal of Social Psychology, Vol.14, 191-201.
Hamilton, D.L. 1979, A cognitive-attributional analysis of stereotyping. Advances in experimental social psychology, Vol.12, 53-84.
Hamilton, D.L. (Ed.) 1981, Cognitive processes in stereotyping and intergroup behavior. Hiilsdale, NJ: Erlbaum.
Hamilton, D.L. 1988, Understanding impression formation: What has memory research contributed? In P.R. Solomon, G.R. Goethals, C.M. Kelley, & B. Stephens (Eds.). Memory - An interdisciplinary approach. NY: Springer-Verlag.
Hamilton, D.L., Gifford, R.K. 1976, Illusory correlation in interpersonal perception: Cognitive basis of stereotypic judgments. Journal of Experimental Social Psychology, Vol.12, No.4, 392-407
Hamilton, D.L., Sherman, S.J. 1988, Illusory correlation: Implications for stereotype theory and research. In D. Bar-Tal, C.F. Graumann, A.W. Kruglanski, & W. Stroebe (Eds.) Stereotypes and prejudice: Changing conceptions. New York: Springer-Verlag. Pp. 59-82.
Hastie, R. 1988, A computer simulation model of person memory. Journal of Experimental Social Psychology, Vol. 24, No. 5, 423-447.
Hintzman, D.L. 1986,"Schema abstraction" in a
multiple-trace
memory model. Psychological
Review, Vol.93, 411-428.
Hintzman, D.L. 1988, Judgments of frequency and recognition memory in a multiple-trace memory model. Psychological Review, Vol.95, 528-551.
Mullen, B., Johnson, C. 1990, Distinctiveness-based illusory correlations and stereotyping - A meta-analytic integration. British Journal of Social Psychology, Vol.29, Mar, 11-28.
Smith, E.R. 1991, Illusory correlation in a simulated examplar-based memory. Journal of Experimental Social Psychology, Vol.27, No.2, 107-123.
�Q�D�P�D�Q�@�O�W�c�̋ώ����F�m�iOut-Group Homogeneity�j
�Q�D�P�D�Q�D�P�@���W�c(in-groups)�^�O�W�c(out-groups)
�F�m��̓���
(1) ���W�c���X��(in-group favoritism) �`�@Tajfel (1982)
(2) �O�W�c�������ώ��ƌ���X��
�y��z
�E�P�l�̈ӌ����W�c�S�̂Ɉ�ʉ�����X���́A���W�c���O�W�c(����w)�ɑ��č����B
�@�iQuattrone & Jones,1980�j
�E���q�w���B�t�@�b�V������w�K�ԓx�Ɋւ��A�����̗������ɂ̓��@���G�e�B������Ǝv���B
�@���������C�o�����̐����͋ώ��I���Ǝv���B�iPark & Rothbart,1982�j
�E�p�[�\�i���e�B�A�s���̓����̈Ⴂ����W�c�����ɑ��Ă��m�o���₷���B
�@(Jones et al,1982; Park & Rothbart,1982)
�Ȃ����H
�Q�D�P�D�Q�D�Q�@Linville �� (1989) �̃��f��
differential familiarity �����F����W�c�̐����ւ� familiarity �������Ƃ��̏W�c�ւ̕����idifferentiation�j�ƕψِ��ivariability�j�̒m�o�����܂�B
���Q�̕����m�o�̑��x
�ip1, ..., pm�j�F�������������鑮���̒m�o�������z
pi�F���̑����̐������́A�߂����ꂽ�䗦
�P�D�o���F�����m���iprobability of differentiation�j
�o���@���@�P�|�������Q�D
�m�G���g���s�@�d�@���@�|�������E�����������@�ɑ�������B�n
�Q�D�u�����F�m�o���ꂽ�ψِ��iPerceived Variability�j
�u�����@���@�������i�w���|�l�j�Q�D
�������A�l�@���@�������E�w���D�iin-group favoritism �̎w�W�j
�o���Ƃu�����͕ʂł���B
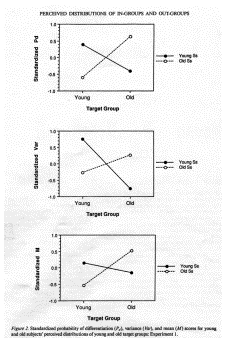
�Q�D�P�D�Q�D�R�@Linville �� (1989) �̎���
�Q�~�Q�̔팱�ҊԌv��
�Q�W�c�@�|�@�팱�ҏW�c�ƑΏۏW�c
�W�̓����ifriendliness, motivation,...�j�@�V�����ł̑���
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�����P �����Q �����R
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�W�c �@�@�@�@old/young �@�@�@Anerican/Irish �@�@�@�����^�j��
�o�� �� �� �~
�u���� �� �~ �~
in-group �� �~ �~
favoritism
|
|
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
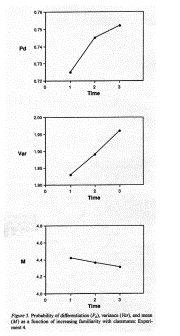
�i�������P�j �i�������S�j
�����S
�����F�������̏W�c�ւ� familiarity �̑���ɂ���āA���̏W�c�����ւ̂o���A�u�����͍��܂�B
�W�c���S���w����N���X�i�C�G�[����w�j
���ʁF �E�������x���B
�E �l�͎���ɒቺ�����B�i���Ԃւ̊��ҊO��^�����H�j
�Q�D�P�D�Q�D�S�@Linville �� (1989) �̃��f���i�Q�j
���@���f���̑O��
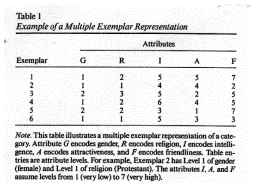
(1) Multiple Exemplar Representation
�@�P�D�Љ�I�J�e�S���[�̒m���́A�J�e�S���[ exemplar �̃��X�g�ɂ���āA�����L���i�k�s�l�j�̒��ŕ\�����B
�@�Q�D�e�J�e�S���[ exemplar �� a feature set �Ƃ��ĕ\�����B
(2) �w�K�E�L���̉ߒ��@�`�@Hintzman (1986) �̃��f��
|
|
�@�w�K
�@�@Plearn �F�@������Ԃŏo��������� exemplar ���k�s�l�ɒ��������m��
�@�@ exemplar �̋ɒ[���ƂƂ��ɍ��܂�B
�A�Y�p
�@�@PForget�F�@�O���Ԃł̋L�����Ղ������ԂŖY�p�����m��
�B��(Retrieval)
�@�@exemplar �� �L�� probe �ɂ���čĐ������i�k�s�l�ɂ����Ċ����������j�B
�@�@PRetrieve�F exemplar �̋ɒ[���ƂƂ��ɍ��܂�B
�@�@������������ exemplar �́u���x�v�����B
(3) ���z�m�o�̌`��
�E���鑮���l�����J�e�S���[�����̒m�o���ꂽ�䗦�́A�r�`�r�ɔ�Ⴗ��B
�b���F�J�e�S���[�����b�̂�����
�`���F�����`�̂�����
�r�`�r�i�b��, �`���j�F�`���̒l���Ƃ�J�e�S���[�b���̑S exemplars �̊��������x�̍��v
�o�i�`���b�b���j�F�`���̒l���Ƃ�b�������́A�m�o���ꂽ�䗦
�o�i�`���b�b���j���r�`�r�i�b��, �`���j�^�����r�`�r�i�b��, �`���j
���@�V�~�����[�V����
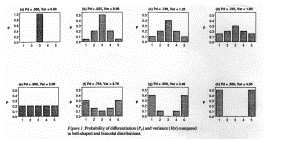
�E�����̂R�̊m�����z�F Bell / Skewed / Bimodal
�E�P���Ԃ͂Q�i�K�ɕ������D
�@�@(1) �w�K�i�K�Fexemplars �ɏo��A�L����Y�p��������B
�@�@(2) ����i�K�Fexemplar �̑����̕��z�𐄒肷��B
�E�T����
�E�Q�����F�b(�m�����z)�ƂP�̂`�i�V�����j
�EPLearn = 0.9 if �ɒ[��exemplar (1 or 7)
0.5 if �ɒ[�łȂ� exemplar (2�`6)
�EPForget = 0.1
�EPretrieve = 0.95 if �ɒ[��exemplar (1 or 7)
0.75 if �ɒ[�łȂ� exemplar (2�`6)
0 if probe �ɍ���Ȃ� exemplar
�E�S�~�R�̗v���z�u
�@(1) Familiarity�F�o� exemplars �̐��@�@�Q�^�T�^�P�O�^�Q�O
�@(2) �m�����z�FBell / Skewed / Bimodal
�������ƂɂP�O�O�̌J��Ԃ�
���@����
(1) �o���Ƃu������ Familiarity �ƂƂ��ɑ���
(2) �o���Ƃu�����ւ̌��ʂ� Familiarity �ƂƂ��ɒ���
(3) �u�������o���ɑ��AFamiliarity �̌��ʂ͋����B
(4) �u�����Ƃo���͕�
�@�@Bell �� Skewed �̕��z�ł͗��҂̑��ւ� 0.3 �` 0.6
�@�@Bimodal �ł͕��̑���
(5) Familiarity �͂l�ɂ͌��ʂȂ�
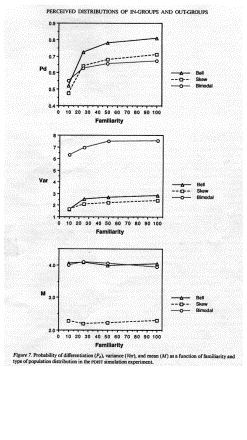
���@�������ʂ̐���
�V�~�����[�V�������ʂ͎�v�Ȏ������ʂ��������B
(1) �o���Ƃu������ Familiarity �������i���W�c�A�W�̐i�s�j�ƍ����B
�@�@�����P�A�Q�A�S
(2) �o���Ƃu�����ւ̌��ʂ̒����@���@���^�O�W�c�łƂ��� Familiarity �����܂�A�����o�Ȃ��B�i�����R�j
(3) �o���̕����u�������Familiarity �̌��ʂ��o�₷���B�i�����Q�j
�Q�l����
Jones, E.E., Wood, G.C. & Quattrone, G.A. (1981) Perceived variability of personal characteristics an in-groups and out-groups. Personality and Social Psychology Bulletin, 7, 523-528.
Linville, P.W., Fischer, G.W. & Salovey, P. (1989) Perceived distributions of characteristics of in-group and out-group members: Empirical evidence and a computer simulation. Journal of Personality and Social Psychology, 57, 165-188.
Park, B. & Rothbart, M. (1982) Perception of out-group homogeneity and levels of social categorization. Journal of Personality and Social Psychology, 42, 1051-1068.
Quattrone, G.A. & Jones, E.E. (1980) The perception of variability within in-groups and out-groups. Journal of Personality and Social Psychology, 38, 141-152.
Tajfel, H. (Ed.) (1982). Social identity and intergroup relations. Cambridge: Cambridge Univ. Press