�Љ�S���w����u�`�F�@�u�`����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�Q�O�O�O�N�@�U���P���i�ؗj�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���؉p��
2.3�@�W�c�ߒ�
2.3.1�@�W�c���c
2.3.1.1�@�w�i
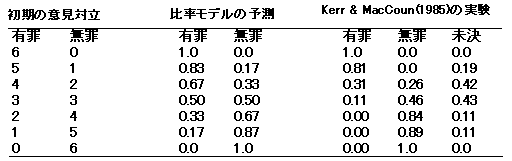
�E�W�c���c�̌��ʂ͐����̏����̈ӌ����z����m���I�ɗ\���ł���B�i���}�j
�E�������u���e���ʁv

���@�B���ꂽ�v���t�B�[���ihidden profile�j
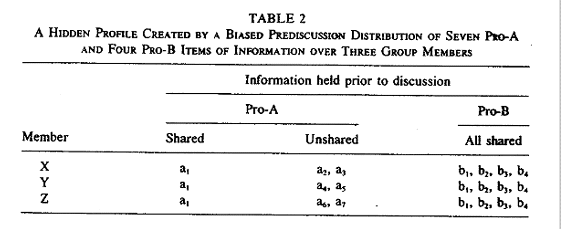
TABLE 1�F�����w�A�x�A�y�B�@�I����A�A�a�B
�E�`�ɗL���ȏ��͂V�@�|�@�����P�i���P�j�������S���ɋ��L����Ă���B
�E�a�ɗL���ȏ��͂S�@�|�@�����P�i���P�j�������S���ɋ��L����Ă���B
���@���̏ꍇ�A�c�_�O���c�_����A�S�����`��I�Ԃ��낤�B
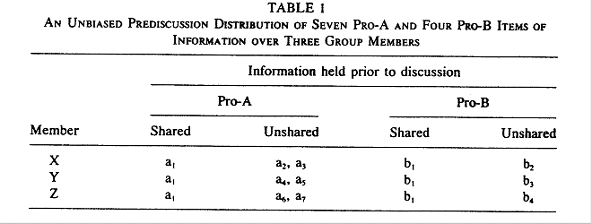
TABLE 2�F�@�B���ꂽ�v���t�B�[��
�E�`�ɗL���ȏ��͂V�@�|�@�����P�i���P�j�������S���ɋ��L����Ă���B
�E�a�ɗL���ȏ��͂S�@�|�@���̂��ׂĂ��S���ɋ��L����Ă���B
���@�c�_�O�͂a���L���B���������c�ɂ���ď���L�������a���I���͂��B
�@�@�@���A�W�c���c�ɂ���Ă��A�B���ꂽ�v���t�B�[���͕K���������炩�ɂȂ�Ȃ��B
Stasser & Titus(1985) �̎���
�@�E�S�l�W�c�̂r��
�@�E3�l�̌��ҁi�`�A�a�A�b�j����K�C�ҁi�w��������j��I�ԁB
�@�E�`�̒����������B
�@�E3�����i���\�j
Shared�F���ׂĂ̏��������L����Ă���B
Unshared/Concensus, Unshared/Conflict�F�B���ꂽ�v���t�B�[������

�@���ʁF���\

�@���@�W�c���c�ɂ���Ă��A�B���ꂽ�v���t�B�[���͍�������Ȃ��B
�Ȃ����H
�P�D���L���ꂽ����c�ɏo�₷���B
�Q�D�����͌��݂̎����̍l�����x����������Đ����₷���B
2.3.1.2 Stasser(1988) �̃V�~�����[�V�����iDISCUSS ���f���j
�����f���̍\��
�i�P�j����
�i�P�E�P�j�ۑ�p�����[�^
���c�̑I����
�e�I�����̏�ڐ�
��ڂ� valence
�����Ԃ� valence �̕��U
�i�P�E�Q�j���c�p�����[�^
�W�c�T�C�Y
�Q���x
���c�W�c�����̎Q���x�̓����N�Â�����B
�o���F�� �Ԗڂ̃����N�̐����̎Q���m���A���F�Q���p�����[�^�A���F�W�c�T�C�Y
�o���@���@�����^�������A�@���@���@�P�A�Q�A�E�E�E�A���D
�����������قǃg�b�v�����N�̐��������c���x�z����B
���胋�[���F����ɕK�v�ȍŒᐬ����
Advocacy�F���������Ȃ̌��݂̑I�D���ɔ��f��������x
�iAdvocacy / Nonadvocacy�j
Norm�F���鍀�ڂւ̎x���I�����ɂ���č��ڂ� valence �̐����Ԃ̍����k��������x
�iNorm / Nonnorm�j
�i�P�E�R�j�I���T�u���f���F�I�����̕]���̃��f��
�d�`�F�I�����`�ւ́i���鐬���́j�]���A�����F�������`�ɂ��čĐ��������Ԗڂ̏�ڂ�valence
���F���̐������Đ�������ڐ�
���Z�T�u���f�� �d�`�@���@������
���σT�u���f�� �d�`�@���@�������^��
�i�P�E�S�j���c�O�̏�z
�i�Q�j�V�~�����[�V����
�i�Q�E�P�j���c�O�ǖ�
��ڂ̍Đ��F���ڐ��i��ׁA�m�j���傫���قǂ��鍀�ڂ̍Đ��m���i�o���j�͒Ⴂ�B
�o���@���@���^�m�@�{���@�@�i���A���F���̒萔�j
�I�����̕]���F�Đ�����ёI���T�u���f���Ō��߂�B
�i�Q�E�Q�j���c�ǖʁi���Ԃ��ƂɁj
�����ҁF�Q���̊m���ɂ��B
���i�ǂ̏�ځj��b�����H�@�|�@�����̍Đ��ɂ��B
�����������͂��̍��ڂ��Đ����]���̕ω�
�iNorm �̏ꍇ�A������� ���� �͔����҂� ���� �̕����ɓ����B�j
�i�Q�E�R�j���c�I��
��v�iConsensus�j�F���胋�[�����[�����ꂽ�Ƃ�
�s���l�܂�(Stalemate)�F"no decision"
�i�R�j�o��
���c�O�̑I�D���z
�W�c���蕪�z
�Ȃ�
���@�V�~�����[�V�����̎��{
�i�P�j�p�����[�^�ݒ�F�ߋ��̎������ʂ��画�f���A�ȉ��Ă͂߂�B
valence�F�I�����`�̂W�̐��̍��ڂ̂����S�́{�Q�A�c��S�́{�P�D�T
�@�@�@�@�@�@�@�@�@�@�@���̍��ڂ́|�P
valence �̕��U�@���@�P
�Q���p�����[�^�@���@���@0.75
�i�Q�j�Q(Advocacy / Nonadvocacy)�~�Q(Norm / Nonnorm)�~�R(Shared / Unshared-Consensus / Unshared Conflict)
���@����
�E�f�[�^�iTABLE 4�j�Ƃ̓��Ă͂܂肪�ǂ������̂� Nonadvocacy-Norm ���f���� Advocacy-Norm ���f��
���@Norm �̗v�����Ȃ��ɏ����������ł́A�f�[�^�̂悤�� Consensus �͓����Ȃ��B
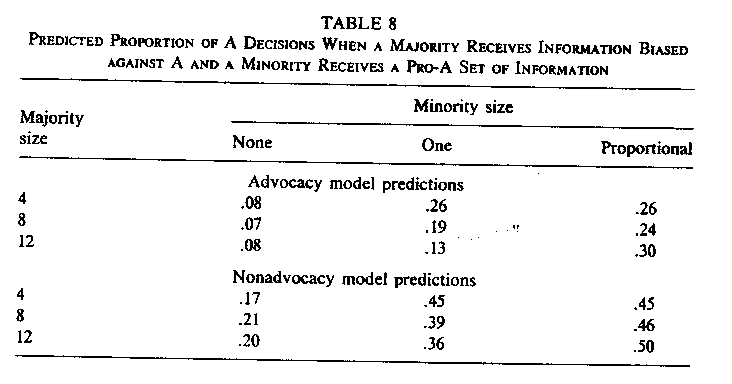
�ETABLE 7�FNonadvocacy-Norm ���f���� Advocacy-Norm ���f���Ɋ�Â��\��
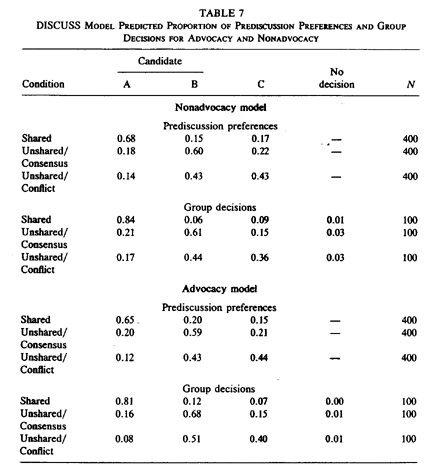
���@�lj��̃V�~�����[�V�����F�B���ꂽ�v���t�B�[�����ł̏����h�̌���
�����h�T�C�Y�F�S�^�W�^�P�Q
�����h�T�C�Y�F�O�^�P�^�����h�̂S���̂P
���ʁF�����h�͉B���ꂽ�v���t�B�[���̔����ɍv������iTABLE 8 �|�@���c�ł`���I���䗦�j�B
Nonadvocacy-Norm ���f���œ��ɏ����h�̌��ʂ͑傫���B
�Q�l����
Baron, R.S., Kerr, N. & Miller, N. (1992) Group process, group decision, group action. Buckingham: Open Univ. Press.
Kerr, H.L. & MacCoun, R.J. (1985). The effect of jury size and polling method on the process and product of jury deliberations. Journal of Personality and Social Psychology, 48, 349-363.
Larson, Jr., J.R. (1997). Modeling the every entry of shared and unshared information into group discussion: A review and BASIC language computer program. Small Group Research, 28, 454-479.
Stasser, G. (1988). Computer simulationj as a research tool: The DISCUSS model of group decision making. Journal of Experimental Social Psychology, 24, 393-422.
Stasser, G. & Titus, W. (1985). Pooling of unshared information in group decision making: Biased information sampling during discussion. Journal of Personality and Social Psychology, 48, 1476-1478.
2.3.2�@�R�~���j�P�[�V�����l�b�g���[�N�i�b�m�j
2.3.2.1�@�b�m��������
���@�R�~���j�P�[�V�����E�l�b�g���[�N������������
�@1.�ʒu���قȂ鐬�����ʁX�̏������B
�@2.���𑍍����ĉ����o���ۑ�Ɏ��g�ށB
�@3.���̓l�b�g���[�N��ʂ��ē`�B�����B
���@�l�b�g���[�N�̌^�Ɖۑ�
�E��ȃl�b�g���[�N�̌^�F�@�ԗ^(Wheel)�A���^(Chain)�A�x�^�A�~�^(Circle)�A
�@�@�@�@�@�@�@�@�@�@�@�@���S�A���^(Completely Connected, ComCon)
�E�l�b�g���[�N�̒��S��
�E�l�b�g���[�N��̈ʒu�F���S�I�^���ӓI
�E�ۑ�F �P���@�|�@���ʃV���{���ۑ�
�@�@�@�@�@ ���G�@�|�@�Z�p�v�Z�ۑ�A�Ȃ�
���@��v�Ȏ����I�m��(Shaw, 1964�@�Ȃ�)
�@���S���̍����b�m(e.g., Wheel �^)�Ő����Ԃ̊K�w�I�Ȗ��������������₷���B
�A���Ɂu���[�_�[�v�͒��S�I�ʒu�ŏo�����₷���B
�B���S���̍����b�m�͒P���ȉۑ�ŁA���S���̒Ⴂ�b�m�͍���ȉۑ�ŁA�����I�ƂȂ�B
�C�����̖����x�͂b�m�̌^��ʒu�Ɉˑ�����B���S���̍����b�m�̐�������ӓI�ʒu�̐����͖����x���Ⴂ�B
2.3.2.2�@�b�m�̃V�~�����[�V�������f���i����, 1999�j
���@���@�|�@�b�m�����̒m���͔팱�҂̓��L�̐S���ߒ��̌��ʂ��A�\���I�v���̌��ʂ��H
���@���Ԃ͒Z���P�ʎ��ԁi�X�e�b�v�j���Ƃɗ��U�I�ɐ���
���@���i�b�m�Ɖۑ�j�v��
�i�P�j�b�m�F�@�m�~�m��2�l�i�O�P�j�s�� N�@N = (nij) �B
�E�ʒu i ����ʒu j �ւ̏��o�H���J���Ă���Ƃ� nij = 1
�E���Ă���Ƃ� nij = 0 �ł���(������ nij = 0, i=j)�B
�E
�m�i���z�팱�҂̐��j�Ƃb�m�̌^�@�|�@���R�ɕύX�ł���B
�E�o�����I���o�H����Ȃ�b�m�i
N �͑Ώ̍s��j�������l����B
�i�Q�j�ۑ�
�@�`���I�ȋ��ʐ�
1.�e�팱�҂�������ԂŌŗL�́i���̔팱�҂������Ȃ��j�ۑ�������B
2.�S���̉ۑ�����W�߂Ă͂��߂ĉۑ�̉����o����B
3.�S���������҂ɉ���������_�ʼnۑ萋�s�����������Ɣ��f����B�i�P�Z�b�V�������I���j
�@��������x�F�@���ׂĂ̏����W�߂����z�팱�҂��P�l�ʼn�������̂ɗv������Ҏ���
�K���}���z�i�������Ԃ̊m�����z�j�ɂ��������Ɖ���
���@���z�팱�҂̉ۑ�s��
�i�P�j���
�@�E���z�팱�҂��I���ǖ������s�ǖ��Ɍ��݂ɓ���B
�I���ǖʁ@�|�@���s���ׂ���Ƃ���������Ƃ��P�I�ԁB
���s�ǖʁ@�|�@��Ƃ𐋍s
�@�E�I���ł����Ƃ͎��̂S��ނ���
�@���`�B�@�����̉ۑ���������͑��҂��������ۑ�����A�I�������P�l�̑��҂ɑ���B
�A���@�܂����Ă��炸�A���ׂẲۑ����ۗL������ԂőI���ǖʂɂ��鉼�z�팱�҂͊m�� P(S) �ʼn�I������B��I������Ǝ��X�e�b�v�ȍ~�̐��s�ǖʂʼn��z�팱�҂͉ɐ�O����B
�B�B�����@�����ʼn����o�������҂��������M���邱�Ƃɂ���ĉ������z�����҂́A���̑I���ǖʂŒB����I�сA�������s�ǖʂŒB���������҂ɕ���B���v���Ԃ͂P�X�e�b�v�B
�C��`�B�@�B���̌�͗D��I�ɉ�`�B�Ɉڂ�B���v���Ԃ͂P�X�e�b�v�Ƃ���B
�i�Q�j���z�팱�҂́u�\���v
���̂R��Ԃ�����Ɖ���
�@��ԂP�F�����ł͇B�̉�������A�ۑ���̓`�B�@�ɐ�O����B���͑��҂Ɉˑ�����B�i�g�j
�@��ԂQ�F�Ə�M�̗������s���B�i�f�t�H�[���g�j
�@��ԂR�F�i�Ɖ�`�B�j�ɐ�剻����Ƈ@���s��Ȃ��B�i���S�I�����ւ̍\���j
�E����Z�b�V�������͊e���z�팱�҂̍\����Ԃ͕ω����Ȃ�
�E�ŏ��̃Z�b�V�����ł͑S�����f�t�H�[���g�̏�ԂQ
�E�Z�b�V�����Ԃł̍\���̕ω�
1.��ԂQ�̉��z�팱��
a.���O�̃Z�b�V�����Ŏ����ʼn����o�������𑼎҂Ɉˑ������Ȃ�m��
P(1|2) �ŏ�ԂP�Ɉڂ�B
b.���O�̃Z�b�V�����Ŏ���������ߑ��҂ɉ����ˑ����Ȃ���A�m��
P(3|2) �ŏ�ԂR�Ɉڂ�B
2.��ԂP�Ȃ����R�ɂ��鉼�z�팱�ҁF���O�Z�b�V�����ł̏W�c�̉ۑ萋�s���܂�����Ό��݂̍�Ɣz�u��ύX���悤�Ƃ���B
a.�O��̃Z�b�V�����ŏ�ԂP�ɂ���A���ۑ萋�s���ԁi�X�e�b�v���j���O�X���� N(2|1)�ȏ㑽����Ώ�ԂQ�ɖ߂�B
b.�O��̃Z�b�V�����ŏ�ԂR�ɂ���A���ۑ萋�s���ԁi�X�e�b�v���j���O�X���� N(2|3)�ȏ㑽����Ώ�ԂQ�ɖ߂�B
3.��ԂP�Ȃ����R�ł���Ƃ��A�������Z�b�V�����ł̃X�e�b�v�����O�Z�b�V�����̃X�e�b�v�����������Ȃ�A�e�X�e�b�v�ŁA���z�팱�҂͊m�� P(R) �Ō��ݓ������Ă����Ɓi��ԂP�Ȃ�A�A��ԂR�Ȃ�@�j��I���\�ƍĒ�`����i���̃Z�b�V�����ō\���͏�ԂQ�ɕ��A�j�B
���@�p�����[�^�@
�i�P�j�s���p�����[�^�F�@P(S)�AP(R)�AP(1|2)�AP(3|2)�AN(2|1) �A N(2|3)
P(S)�AP(1|2)�A P(3|2) �̒l�������@���@�W���I�z��ւ̌l�����F���ł̗U����
�i�Q�j���p�����[�^
�@�@1.�W�c�T�C�Y�@���@�T
�@�@2.�b�m�̌^�@���@Wheel�A Chain�A Y�A Circle�A ComCon
�@�@3.���`�B���ԁ@���@���b�Z�[�W�������X�e�b�v���@�{�@���b�Z�[�W���M���̂̎���
���b�Z�[�W���M���̂̎��ԁ@���@�ŏ��X�e�b�v���� 1
���b�Z�[�W���������ԁ@���@�ۑ��ɔ��
�@�@4.���� �@���@�K���}���z�����l
�i�R�j���ԁi�ۑ�̍���x�j�̑���@���@�።��x�����^������x�����^������x����
2.3.2.3�@�V�~�����[�V��������
�i�P�j�œK�s���p�^��
�b�m�͂����Ȃ�s����팱�҂ɑ������H
�b�m�^�ʂɁA���z�팱�҂̍œK�s���p�^���ׂ�B
�œK�@���@�ۑ�������Ԃ̍ŏ���
��`�I�A���S���Y���̓K�p
����(Fig. 1)
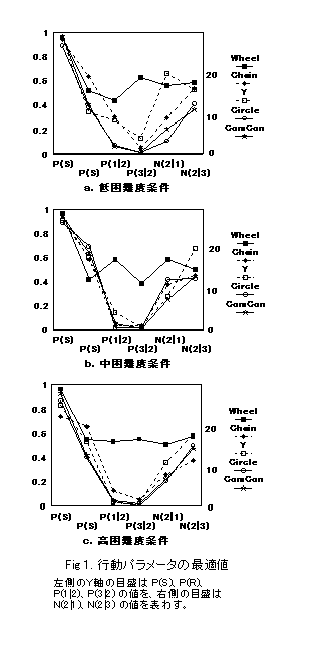
���D P(S) �̒l�͍���x��b�m�^�ɂ�����炸�P�ɋ߂��B
���@�ۑ��W�܂����Ƃ��͑����ɉɓ���̂������I
���D���������ւ̍\���������p�����[�^�m P(1|2) �� P(3|2�n���b�m�̌^�ɂ���ĈقȂ����p�^���������B
���S�������� Wheel �^�@�|�@0.5 �O��
���S�����Ⴂ Circle�AComCon�@�|�@�قƂ�� 0.0
���S�������ԓI�� Chain �� Y �͗��҂̒���
�@���@���S�����Ⴂ�b�m�ɔ�ׁA���S�������� Wheel �ł́A���������ւ̉ۑ�v�����\���I�ɋ����B
�i�Q�j�ۑ��������
�R��ނ̃p�����[�^�łb�m�^���r
�@�E�f�t�H�[���g�FP(1|2) = P(3|2) = 0.0 �Ƃ����BP(S) =
0.93�m�i�P�j�̒�����x�����̑S�̕��ρn
�i���������ւ̍\���Ȃ��j
�@�E������x������ Circle �ł̍œK�l
�@�E������x������ Wheel �ł̍œK�l
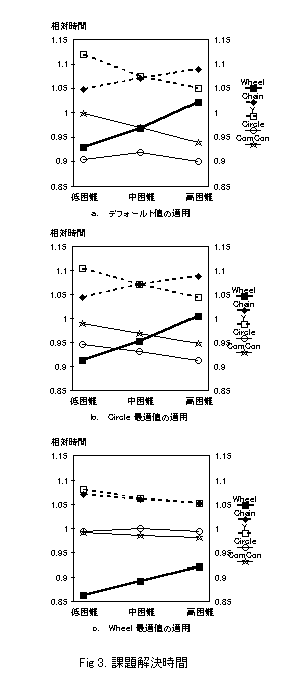
�@���ʁFFig.3�i����x�������Ƃ̕��ς��P�Ƃ����Ƃ��̑��Ύ��ԁj
�E���S�������� Wheel �ł͉ۑ肪����ȂقǑ��Ή������Ԃ͒����Ȃ�B
�E���S�������� Circle�AComCon �ł͋t�B
�@�@������x�A��v�Ȓm���̇B�i2.3.2.1�j�ƕ���
�i�R�j��������
����I�ȂS�̖���
�����ʼn����o�� �o���Ȃ�
���҂ɉ��𑗂� KeyPerson Relayer
����Ȃ� LoneSolver EndPerson
�Q��ނ̃p�����[�^�l
�f�t�H�[���g�l�i���������ւ̍\���Ȃ��j
Wheel �œK�l�i���������ւ̍\���������j
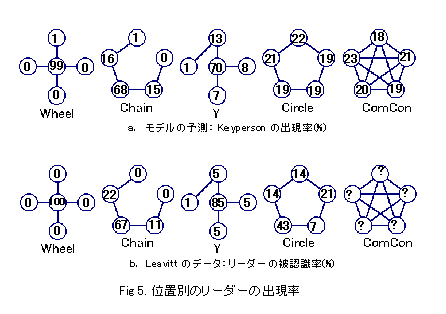
���ʁ@ Fig.4�F�b�m�^�ʂ̖������z
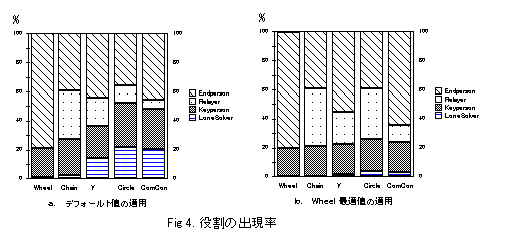
Fig.5a�FKeyPerson �̏o���ʒu
������������������������������������������������������������������
�b�m�^ �f�t�H�[���g�l Wheel �œK�l
������������������������������������������������������������������
Wheel �ǂ���ł��A1 KeyPerson �� 4 EndPersons�i�P�i�K�w�j
Chain EndPerson - Relayer - Keyperson - Relayer - EndPerson�i�Q�i�K�w�j
Y LoneS.�������� ���S�� KeyPerson
Circle �����ґ̐� Chain �Ɠ����Q�i�K�w
ComCon �����ґ̐� Wheel �Ɠ����P�i�K�w
������������������������������������������������������������������
�E�ߋ��̖����\���̋L�q�͏�̕\�͈͓̔��ɂ���B
�EKeyPerson �̏o���ʒu�̗\���͎����l�ƕ�������B
�Q�l����
Bavelas, A. (1950) Communication patterns in task oriented groups. Journal of the Acoustical Society of America, 22, 725-730.
Leavitt, H.J. (1951) Some effects of certain communication patterns on group performance. Journal of Abnormal and Social Psychology, 46, 38-50.
Shaw, M.E. (1964) Communication networks. Advances in Experimental Social Psychology, 1, 111-147.
���؉p�� (1999) �u�R�~���j�P�[�V�����l�b�g���[�N�ɂ�����n���I�W�c�\���@�|�@�V�~�����[�V�����ɂ�镪�́v, �w�Љ�S���w�����x�A14���A�R���A113-122.