社会心理学特殊講義：　講義メモ

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　２０００年　６月８日（木曜）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　高木英至

 2.4　対人過程

2.4.1　親密化の過程

親密化の過程（Acquaintance process）：見知らぬ者同士が知り合い、友人関係を形成する過程

2.4.1.1　経験的知見

☆　２つの要因

　　１．近接性の効果：地理的に近い者同士が友人になりやすい。

                ・接触機会

                ・接触コスト

　　２．類似性の効果：類似した者同士が友人になりやすい。

                ・背景変数：社会階層、学歴、宗教・・・

                ・態度類似性：価値観など

☆　ニューカムの研究（Newcomb, 1961）

                大学の寮での研究　−　半年間の観察（２年）

                １７名（男性）、２つのフロア

　　結果：（多数）

                ・態度類似性の効果が次第に強くなる。

                ・近接性の効果は初期の段階でしか有効ではない。

2.4.1.2　魅力−接触モデル

☆　コンセプト

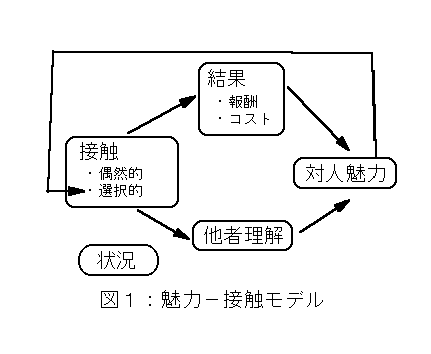１．接触

　　・偶然的接触：近い者と接触しやすい。

　　・選択的接触：好きな者と接触しやすい。

２．接触の効果

　　・結果

                報酬      →　相手への魅力が高まる

                コスト     →　相手への魅力が低下

　　・他者理解　→　相手の態度が分かる。

３．対人魅力（好意）

　　・結果（報酬、コスト）

　　・態度類似性

このモデルがどれほどの予測を生み出せるか？

☆　モデルの特定

１．ある集団内で成員間に接触がある場合を考える。

２．成員は平面上に位置し、位置を移動させない。成員間の距離はユークリッド距離である。

３．態度の次元：各成員の態度は１０の次元からなる。各次元は０か１の値をとる。

４．試行の構成：１つの run は多数の試行からなる。１回の試行は偶然的接触の局面と選択的接触の局面からなる。接触ごとに、その当事者の他者（の態度）理解と魅力の変化が生じる。

５．偶然的接触：ある試行で成員ｉ、ｊ間に偶然的接触が生じる確率 P[i,j] は以下で求める。

             P[i,j] = C₁ /（ｉ、ｊ間の距離の２乗）．　C₁ ：定数

この確率で偶然的接触が生じるペアを乱数で決める。接触が生じる順番も乱数で決める。

６．選択的接触：ある試行で成員ｉがｊに対して選択的に接触しようとする傾向 Prop[i,j] は次式で決める。

 Prop[i,j] = (C₁ + C₂ΣA_ik) * A_ij/ΣA_ik − C₃ * d²_ij.（１２）

                 　　　　　     ^{k    　　         k}

   A_ij : ｊに対するｉの魅力、d_ij : ij間の距離、 C₁ 、C₂、C₃ ：定数

   ただし 0.0 ≦ A_ij、 0.0 ≦ Prop[i,j] ≦ 1.0.

Prop[i,j] ：・他成員に比べ相対的にｊへの魅力（A_ij/ΣA_ik）が高いほど、高くなる。

            　・同時に魅力の絶対的な程度(C₁ + C₂ΣA_ik)が高いほど、高くなる。

距離(d_ij)：接触を思い止める方向に作用する。

ｉ、ｊ間の選択的接触の確率： Prop[i,j] と Prop[j,i] の幾何平均

７．他者理解：一回の接触ごとに成員は相手の各態度次元の値を一定の確率(P_found = .05 )で知る。
・ｊに対するｉの想定類似性：ｉが知っているｊの態度次元の値の中で自分自身と値が同じものの比率

・相手の態度が全く分からない場合は想定類似性は 0.5とした。

８．対人魅力：ｊに対するｉの魅力(A_ij)は類似性に基づく魅力(A1_ij)と報酬性に基づく魅力(A2_ij)の加重平均。

    A_ij = αA1_ij + (1-α)A2_ij.　0.0 ≦ α ≦ 1.0.　

９．類似性に基づく魅力(A1ij)：想定類似性(Asim[i,j])の線形関数（Byrne らの知見）

１０．報酬性に基づく魅力(A2_ij)

・初期値は 3.0

 ・１回接触があれば、接触した成員にある程度の報酬が生じ、報酬性に基づく魅力が次式の inc だけ増大すると仮定。　　  inc = 0.1 * (10.0 − A2_ij).　

また試行ごとに A2_ij は次式の dec だけ減少する。

　　                    dec = 0.2 * (A2_ij − 3.0).

全く接触がなければ A2_ij は初期値に戻る。

・ｉｊ間の接触が良い結果になる確率(P_good)：両者相互の魅力の幾何平均に比例

                             P_good = Sqrt(A_ij*A_ji) / 20.0.

良い結果になれば上記の魅力増大分(inc)は倍増する。

・接触が悪い結果になる確率(P_poor)は P_good と反対に動く。

    P_poor = 1.0 − (1.0 − P_good)/3.0.

悪い結果になれば A2_ij は　0.7 だけ低下する。

2.4.1.3　シミュレーション結果

（１）　升目上の集団における親密化

☆　前提

・２５人の集団成員が５×５の正方形の升目の中に位置する。

・上下左右の隣人との距離は２。

・態度の１０次元の値(1/0)は乱数で決める(p=0.5)。

・α＝0.5 （対人魅力への規定力で態度類似性と報酬性は等しい。）

・１００試行を続ける。

☆　主な結果（モデルの予測）

a.他者の態度理解と他者への魅力は時間とともに向上する。

b.成員ペア間の理解度と魅力のアンバランスは次第に低下する。

c.相手が近接しているほど、および(客観的に)態度が類似しているほど、他者理解と魅力は高い。

d.時間とともに、上記の近接性の効果は低下し類似性の効果は向上する（下図）。

e.中心的位置にいる成員は

　・他者理解の達成度が高く、近接性の制約を受けにくい。

　・相互満足的な(魅力が高く、バランスした)関係を作りやすい。

f.中心的な成員は類似性にしたがい、周辺的成員は近接性にしたがい、他者に魅力を抱く傾向がある。

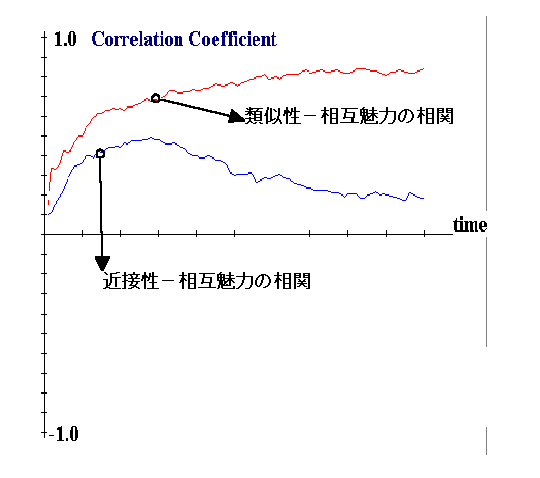
（２）　Newcomb(1961) の観察状況

☆　前提

・成員数：Newcomb(1961) と同じく１７名。

・２階と３階に成員が住む寮を想定。1〜9 の成員は２階、10〜17 は３階。

　floormates であれば相互の距離（の２乗）は２、階が異なれば６、とした。

・成員の態度の値は、第１〜４次元を除いて run ごとに乱数で決める(p=.5)。

　第１〜４次元の態度の値は、階ごとに、全部１の成員と全部０の成員が半々。

・３つのモデル

                α＝ 0.5　→　標準モデル

                α＝ 0.2　→　報酬性モデル（対人魅力への規定力は報酬性が支配的）

                α＝ 0.8　→　類似性モデル（対人魅力への規定力は態度類似性が支配的）

☆　結果（モデルの予測）

　　　→　Newcomb(1961)に報告された主な１４の知見が「質的に」再現されるか否かを調べる。

・標準モデルと類似性モデルは14の知見のほとんどを再現する（次頁、表１）。

　類似性モデルは知見の再現に失敗。

☆　考察

・Newcomb(1961) の状況は態度類似性が支配的であった？

・経験的知見の再現には複雑な心理的仮定がほとんど必要なさそうだ。

・次の２つの心理的傾向の導入は、知見をほとんど変化させない。

　　１．態度変化（Newcomb のＡ−Ｂ−Ｘモデル）：他者と態度が異なる場合、その他者への魅力が高いほど

                その他者の方向に態度を変化させる。

　　　　→態度変化の存在は類似性−魅力の相関をかえって抑制する。

　　２．autism：他者の態度を推論によって想定する傾向

　　　（Ｂの未知の態度次元の値を、Ｂへの魅力度に比例した確率でＡは自分と同じだと推論する、と仮定）

　　　　→autism の存在は近接性−魅力の相関を低める効果をもっただけ。

表１：Newcomb(1961)の知見の再現成績

──────────────────────────────

　　　　              知見　　　　　　　　　　　　　　                         成績

────────────────────────────── 

1.近接性による相互魅力の説明力は初期に高く、                ○

   次第に低下する。

 2.態度類似性による相互魅力の説明力は後期に高まる。    ○

 3.ペア内の魅力の相互性は後期に高まる。                       ○

 4.ペア内の魅力の相互性は中間的な魅力水準で               △

   増大しやすい。

 5.魅力水準が高いペアで、高い魅力相互性は前・後期を      ○

   通じて生じる。

 6.ペア内相互魅力の安定性は後期に高まる。                    ○

 7.魅力が安定的なペアの比率は相互魅力の高･低群で       ○

　多い。

8.特に相互魅力の高い群で魅力が安定的なペアの比率が    ○

   高い。

 9.魅力を感じる他者の順位の安定性は後期に高まる。        ○

10.人気が高いほど魅力順位は安定的である。                    ×

11.人気が高いほど魅力順位の他者との一致度は高い。       ○

12.魅力順位の他者との一致度と人気との相関は次第に       ○

   増加する。

13.高相互魅力ペア数は次第に増加する。                          ○

14.高相互魅力triads数は次第に増加する。             ○

──────────────────────────────

                ○：成立　　×：不成立　　△：見方による

参考文献

Blieszner, R. & Adams, R.G. (1992).  Adult Friendship.  London: Sage.

                （友人関係に関する経験的知見に詳しい。）

Erber, R. & Gilmour, R. (Eds.)  (1994).  Theoretical Frameworks for Personal Relationships.  Hillsdale, N.J.:                            Lawrence Erlbaum.  （対人関係に関する理論的展開に詳しい。）

Newcomb, T.M. (1961). The acquaintance process.  New York: Holt, Rinehart & Winston.

2.4.2　恋愛関係の形成

2.4.2.1　経験的知見：外見的魅力の釣り合い

☆　カップル（恋人、夫婦）間での外見的魅力(physical attractiveness)の釣り合い（matching）＝カップル内相関

                例：Murstein & Christy(1976)

　　・いろんな調査対象者層で観測できる。

　　・ただし釣り合い（相関）の度合は観測によって異なる。

　　（レヴュー：奥田, 1990）

☆　釣り合い仮説（Matching Hypothesis）

３つの形態

　(1) 強い釣り合い仮説：人は自分と外見が釣り合った異性を好む（魅力を感じる）。

　(2) 中間の釣り合い仮説：人は魅力的な相手を好むものの、現実的考慮によって自分と同じ魅力水準の

　　　相手をパートナーに選ぶ。

                パートナーとしての望ましさ　＝　相手の魅力　×　受容の可能性

                （←　達成動機の期待理論：　アスピレーション水準　＝　結果の望ましさ　×　成功確率）

　　　　　望ましい相手でも受容されないと思えばパートナーにしようとはしない(Shanteau & Nagy, 1979)。

　(3) 弱い釣り合い仮説：人は魅力的な相手を好むものの、結果として釣り合いが生じる。

☆　釣り合い仮説の直接的検証(Berscheid ら, 1971; Walster ら, 1966)

　・外見的魅力が高い者はパートナーにも魅力を求める。

　・しかし被験者は、自分の魅力水準にかかわらず魅力が高い者をパートナーに選ぼうとする。

　・魅力が同水準の相手を好きになったり、選んだりする傾向は見出せなかった。

2.4.2.2　Kalick & Hamilton(1986) のコンピュータ・シミュレーション

☆　Kalick & Hamilton(1986)：釣り合いの事実を説明するためには「弱い釣り合い仮説」だけでよい。

前提

　・多数の仮想の参加者（男女、各１０００名）

　・各参加者は魅力水準（１−１０の整数値）を一様分布の乱数で割当てられる。

　・離散的な試行：各試行で各参加者はランダムな組み合わせでデートをする。

　・「カップルの双方が相手を受容」　→　カップル形成　→　接触の対象から外れる。

　・受容の確率　−　相手への魅力に比例

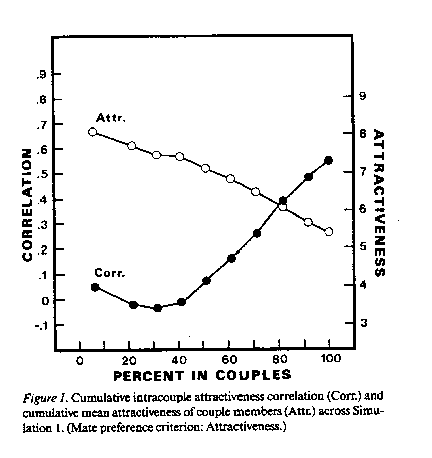
シミュレーション１：人は魅力的な相手を好む、とだけ仮定

　受容の確率　Ｐ_１　＝　(Ａ_P ³ / 1000).　　Ａ_P：相手の魅力水準

　次のように修正

                　　　　Ｐ_1C　＝　(Ａ_P ³ / 1000)^(51-d)/50.　d：デート回数（＝試行数）

                →　５１試行では全員が受容する。

結果：　Figure 1.

・最初は水準が高い者同士が、後には低い者同士がカップルとなる。

・釣り合い（できたカップル間の魅力水準の正の相関）が生じる。

・釣り合いは累積カップル数とともに高まる。

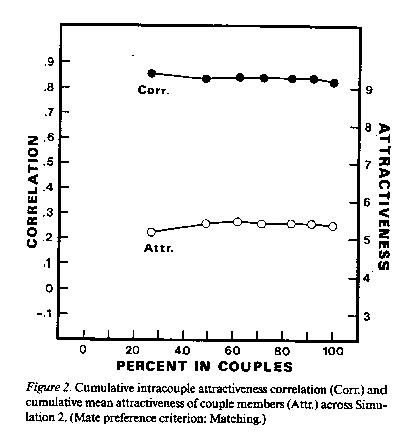
シミュレーション２：人は魅力水準が自分と類似した相手を好む、と仮定

　受容の確率　Ｐ_２　＝　（10 − |Ａ_O−Ａ_P|）³ / 1000.　　Ａ_O：自分の魅力水準、Ａ_P：相手の魅力水準

　修正して、　　Ｐ_２Ｃ　＝　Ｐ_２^(51-d)/50.

結果：Figure 2.

　・釣り合いは終始高い。

　・カップル間の魅力水準にも試行による差はない。

シミュレーション３：シミュレーション１、２の折衷モデル

　受容の確率　Ｐ_３　＝　（Ｐ_１＋Ｐ_２）／２.

　修正して　　　Ｐ_３Ｃ　＝　Ｐ_３^(51-d)/50.

結果：シミュレーション1、2の結果を折衷した傾向を示す。

結論　→　弱い釣り合い仮説だけで現実は説明できる。

☆　Aron(1988) の批判

(a) 魅力水準は一様分布ではなく正規分布となるはず。

　　現実に近い魅力分布を仮定してシミュレーションをやりなおすと、シミュレーション1での相関はほとんど

　　消える。

(b) 現実には魅力評定に測定誤差があるので、魅力の相関は低くなるはずだ。

(c) 相手の選択には魅力以外の要因も入る（例：態度類似性、状況要因）。

　　→　魅力だけが作用すると仮定した Kalick & Hamilton(1986) のシミュレーションは魅力の規定力を

　　　　 過大評価することになる。

(d) 現実には全員がカップルになる訳ではない。　

　　→　全員がカップルにならないとすれば、シミュレーション1での魅力の釣り合いは低下する。

(e) デート回数を考慮した修正の効果が正当化できるか？

魅力の釣り合いに対する別の説明可能性

(1) カップルは一緒に暮らすことによって似てくるのかも知れない。

(2) 印象管理戦略　→　人は魅力的な人に会うときは外見を魅力的にしようとする。

(3) 接触に対する社会的制約：魅力水準が同等な者と接触機会が多い。

(4) 「中間の釣り合い仮説」が妥当する可能性

☆　Kalick & Hamilton(1988) の反論

・ Aron(1988) の指摘 (a)、(d)、(e) を考慮してシミュレーションをし直しても、結果に大きな変更はない。

・(c) について、将来的には考慮すべきだろう。

・(b) について、魅力評定の信頼性は Aron(1988) の計算よりも高い。

参考文献

Aron, A. (1988)  The matching hypothesis reconsidered again: Comment on Kalick and Hamilton. Journal of Personality and Social Psychology, 54, 441-446.

Berscheid, E., Dion, K., Walster, E., & Walster, G.W. (1971). Physical attractiveness and dating choice: A test of matching hypothesis.  Journal of Experimental Social Psychology, 7, 173-189.

Clark, M.S. & Reis, H.T. (1988)  Interpersonal processes in close relationships. Annual Review of Psychology, 39: 609-672.

Kalick, S.M. & Hamilton III, T.E.  (1986)  The matching hypothesis reexamined. Journal of Personality and Social Psychology, 51, 673-682.

Kalick, S.M. & Hamilton III, T.E.  (1988)  Closer look at a matching simulation: Reply to Aron. Journal of Personality and Social Psychology, 54, 447-451.

Murstein, B.I. & Christy, P. (1976)  Physical attractiveness and marriage adjustment in middle-aged couples.  Journal of Personality and Social Psychology, 34, 537-542.

奥田秀宇 (1990)  「恋愛における身体的魅力の役割　−　釣合仮説を巡って」　『心理学評論』、Vol.33, No.3, 373-390.

Shanteau, J. & Nagy, G.F. (1979)  Probability of acceptance in dating choice. Journal of Personality and Social Psychology, 37, 522-533.

Walster, E., Aronson, V., Abrahams, D. & Rottman, L. (1966)  The importance of physical attractiveness in dating behavior. Journal of Personality and Social Psychology, 4, 508-516.

2.4.3　恋愛市場モデルに基づくシミュレーション

2.4.3.1.　恋愛市場モデル−　図２

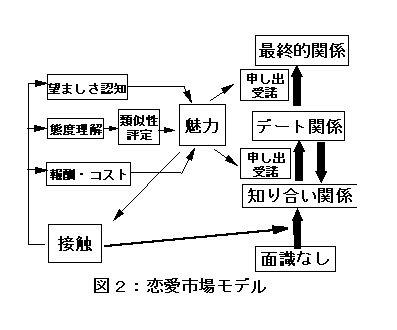
１．関係の段階

　　面識なし

　　知り合い関係

　　デート関係

　　最終的関係　−　市場から抜ける。

２．プロポーズ、受諾確率

　　相手への魅力とともに高まる。

３．魅力の規定因

　　ａ．望ましさ（外見、など）

　　ｂ．態度類似性

　　ｃ．接触の結果（報酬、コスト）

４．接触の規定因

　　ａ．偶然的接触確率　−　一定

　　ｂ．選択的接触確率　−　魅力とともに高まる。

2.4.3.2.  シミュレーション：釣り合いの規定因

前提

　望ましさと類似性に基づく魅力：attr1  = α･望ましさ評価  ＋(1-α)･類似性･10、α=0.5

　報酬経験に基づく魅力：attr2

　総合的魅力（Tattr）：Tattr = β･attr1 ＋(1-β)･attr2、β = 0.5

要因

　１．プロポーズ権要因

                平等条件：男女にプロポーズ権がある

                不平等条件：プロポーズ権があるのは男性だけ。（拒否権は女性にもある。）

　２．接触範囲要因

                広範囲条件

                狭範囲条件

　３．準拠点要因

                準拠条件：準拠点が作用

                通常条件：作用せず

結果

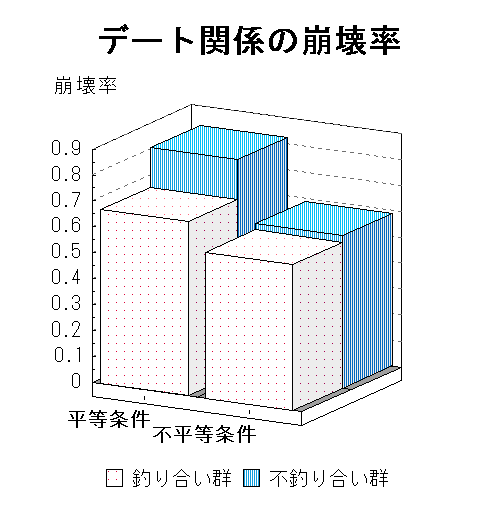
１．デート関係の崩壊率

　・不釣り合いな関係は崩壊しやすい。（〜公平理論）

　・ただし不平等条件では、釣り合い／不釣り合いの差がない。

　・不平等条件では崩壊率が低い。

 ・接触の範囲が広いと崩壊率が低い。

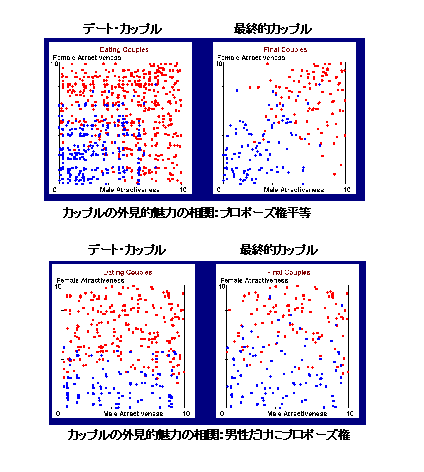
２．釣り合い傾向

 　・カップル間の望ましさは釣り合う。

　・釣り合いは最終的関係で強い。

　・不平等条件では釣り合いが抑制される。

　・準拠点が作用すると釣り合いが高まる。

結果の含意　→　釣り合いの度合は要因に依存する。

釣り合いの規定因

　１．個人的要因

                望ましさへの反応感度

                戦略・志向

　２．関係的要因

                関係の深さ

　３．構造的要因

                社会の segmentation

                望ましさの分布

                接触機会（初期のみ）

                プロポーズ権の平等性

2.4.3.3　恋愛志向の進化

恋愛志向は集合的に決まる。

社会状況に適した志向が生き残る。

前提

　・世代間の観察学習

　・成功例が失敗例にとってかわる。

　・観察学習の対象（モデル）＝同性、同じ望ましさ階層

　・成功指標：α・相手の望ましさ＋（１−α）・態度類似性

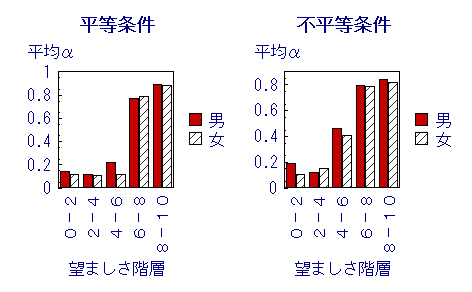
分析１：α（望ましさを求める程度）の変化

　・望ましい者ほどαが高い。

　・不平等条件の男でαがやや高まる。

分析２：matching戦略の採用

　matching戦略：選択の相手を望ましさが自分と近い異性に限定する。

　matching戦略採用率５０％から出発

　・望ましさの低い者はmatching戦略を放棄する。

　・不平等条件の女性はmatching戦略を保持する。

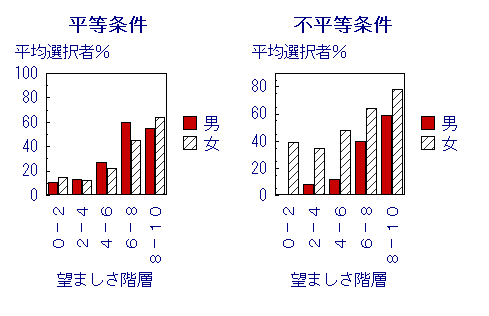
分析３：消極戦略の採用

　消極戦略：恋愛に消極的（プロポーズ率、受諾率が低い。）

　・消極戦略は広まらない。

　・不平等条件の女性は消極戦略を放棄しない。

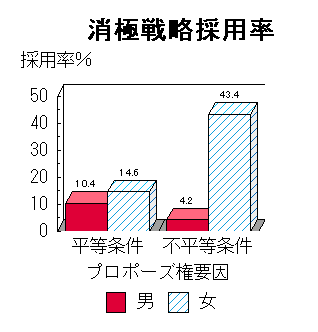
結果の含意

分析１　→　望ましさによる市場分化

分析２　→　matching戦略を採用するのは一部

分析３　→　消極戦略は部分的にしか生き残れない
プロポーズ権が不平等であることの効果

                男：図々しくなる（αが高い）。

                女：matching、消極戦略を放棄せず。